Article 43

A study of some general integrals which contain the wide Denjoy integral

Real Analysis Exchange 26 (2000/2001), no. 1, 51-100.

Mathematical reviews subject classification: 26A39; 26A42; 26A45.

Abstract

In this paper, using Thomson's local systems, we introduce some very general integrals, each containing the wide Denjoy integral:

the $\small \bigl [{\mathcal S}_1 {\mathcal S}_2 {\mathcal D}\bigr ]$ -integral (of Lusin type);
the $\small \bigl [{\mathcal S}_1 {\mathcal S}_2 {\mathcal V}\bigr ]$ -integral (of variational type);
the $\small \bigl [{\mathcal S}_1 {\mathcal S}_2 {\mathcal W}\bigr ]$ -integral (of Ward type);
the $\small \bigl [{\mathcal S}_1 {\mathcal S}_2 {\mathcal R}\bigr ]$ -integral (of Riemann type).

We prove that in certain conditions the integrals $\small \bigl [{\mathcal S}_1 {\mathcal S}_2 {\mathcal V}\bigr ]$ and $\small \bigl [{\mathcal S}_1 {\mathcal S}_2 {\mathcal W}\bigr ]$ are equivalent (it is shown that the first integral satisfies a Saks-Henstock type lemma).

For the $\small \bigl [{\mathcal S}_1 {\mathcal S}_2 {\mathcal R}\bigr ]$ -integral we only show that it satisfies a quasi Saks Henstock type lemma (see Lemma 7.4).

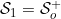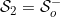Finally, if $\small{\mathcal S}_1 = {\mathcal S}_o^+$ and $\small{\mathcal S}_2 = {\mathcal S}_o^-$ we obtain that the integrals

$\small \bigl [{\mathcal S}_o^+ {\mathcal S}_o^-{\mathcal V}\bigr ]$ , $\small \bigl [{\mathcal S}_o^+ {\mathcal S}_o^-{\mathcal W}\bigr ]$ and $\small \bigl [{\mathcal S}_o^+ {\mathcal S}_o^- {\mathcal D}\bigr ]$

are equivalent.

In fact the $\small \bigl [{\mathcal S}_o^+ {\mathcal S}_o^-{\mathcal D}\bigr ]$ -integral is exactly the wide Denjoy integral.

But the equivalence of the three integrals above with the $\small \bigl [{\mathcal S}_o^+ {\mathcal S}_o^- {\mathcal R}\bigr ]$ -integral follows only if we assume the additional condition that the primitives of the $\small \bigl [{\mathcal S}_o^+{\mathcal S}_o^- {\mathcal R}\bigr ]$ -integral are continuous (see Theorem 11.1)