|
Contact |
This email address is being protected from spambots. You need JavaScript enabled to view it.
|
|
 |
Real Functions - Current Topics
Lecture Notes in Mathematics 1603, Springer Verlag 1995

The preface
The Lebesgue integral, introduced at the beginning of our century has been a turning point in the development of the Mathematical Analysis in general and for the evolution of the notion of integral in particular. Most books devoted in our century to the theory of the integral are dominated by the ideas having their source in Lebesgue's theory. One of these ideas is the property of absolute convergence of the Lebesgue integral (f is integrable if and only if |f | is integrable), very convenient in most fields of Functional Analysis.
However it is well-known, the theory of trigonometric series and other lines of thinking in Mathematical Analysis lead to the introduction of some generalizations of the Lebesgue integral that are no longer absolutely convergent. The first monograph giving a clear account of these nonabsolute integrals (for instance, Perron's integral and Denjoy's integrals) was due to Stanislaw Saks (Theory of the Integral, 2nd. rev. ed. Monografie Matematyczne, PWN Warsaw 1937). But this phenomenon remained an isolated one; most subsequent books devoted to the theory of the integral ignored the nonabsolute integrals, despite the fact that the literature devoted to them became richer and richer. The aim of the present monograph is just to fill this gap.
We don't ignore the existence of several books concerned in the last decade, with the Kurzweil-Henstock integral, one of the most important nonabsolute integral; but as it is well known, this integral is equivalent to the Perron integral, while our aim is to go further and to cover the next steps in the literature devoted to nonabsolute integrals. In this respect, an outstanding result is the Foran integral (1975), which is a classical generalization of the Denjoy integral in the wide sense. In 1986, Iseki gave another generalization of the Denjoy integral, and called it the sparse integral. However neither of the two generalizations is contained one in the other. Our purpose is to give a descriptive definition of an integral which contains both, Foran's integral and Iseki's integral. In order to do this, and also to classify the so many existing integrals, it seems natural to perform a very deep study on the large number of classes of real functions, which have been introduced in this context (many of them by the author himself).
Since there are necessary a lot of examples and counterexamples (66) to illustrate the properties of various classes of functions, we considered that it would be useful to gather them in a separate chapter, at the end of the book.
To show the uniqueness of the integrations we need several monotonicity theorems, which are studied in Chapter IV. But this part of the book is also interesting by itself, because we give there strong generalizations of many monotonicity theorems, studied in the books of Saks (Theory of the Integral, 2nd. rev. ed. Monografie Matematyczne, PWN Warsaw 1937), Bruckner (Differentiation of Real Functions, Lect. Notes in Math., 659, Springer-Verlag 1978) and Thomson (Real functions, Lecture Notes in Mathematics, 1170, Springer-Verlag 1985) (often Lusin's condition (N) is replaced by Foran's condition (M)).
Thomson introduced in 1982 the notion of local systems, trying to unify the theory of the derivation and integration processes, and to indicate the close connection between them (Derivation bases on the real line, I and II. Real Analysis Exchange, 8 (1982/3), 67-208, 280-442; Real Functions, Lecture Notes in Mathematics, 1170, Springer-Verlag 1985). Since then many authors used local systems in the study of continuity, derivability, monotonicity and integrability. Beside monotonicity, we use local systems to investigate complete Riemann integrals (Kurzweil-Henstock integrals). We give Perron and descriptive type definitions for these integrals, and show that they are contained in Denjoy type integrals (in the wide sense).
Chapter V we extend the classical result of Nina Bary, that a continuous function on an interval is the sum of three superpositions of absolutely continuous functions (Mémoire sur la représentation finie des fonctions continues, Math. Ann., 103 (1930), 185-248 and 598-653). We also show the close relationship between Nina Bary's wrinkled functions and Foran's condition (M).
The present monograph can be used as a textbook of a special course of Mathematical Analysis, devoted to graduate and postgraduate students in Mathematics. By its systematic nature and by the great attention given to examples, this monograph should be appropriate for all students who want to deepen their knowledge and understanding of one of the most important chapters of Mathematical Analysis.
In writing this monograph, we have benefited from discussions with several persons. Let us mention first our ten month stay at the Michigan State University, East Lansing, 1991-1992, giving us the opportunity of frequent talks with Professor J.Marik and Professor Clifford E.Weil. During the same stay we met Professor Paul Humke who was the first to suggest us the idea of writing this monograph, after an attempt to write a survey article on a similar topic.
We received a significant help from the anonymous reviewers of this monograph, for editorial purposes.
Professor Solomon Marcus, who guided us in our first steps in Real Analysis as well as in our Ph.D. thesis, helped us in many respects in improving this monograph.
The Springer Publishing House gave us an important support in improving the final presentation.
To all these persons, to Springer Publishing House and last but not least to our wife Gabriela Ene, who took care of technical aspects related to English and printing, we express our warmest thanks.
Vasile Ene
The contents
| 1 |
|
Preliminaries |
1 |
| |
1.1 |
Notations |
1 |
| |
1.2 |
The δ-decomposition of a set |
2 |
| |
1.3 |
Notions related to Hausdorff measures. Conditions f.l. and σ.f.l. |
2 |
| |
1.4 |
Oscillations |
4 |
| |
1.5 |
Borel sets Fσ, Gδ Borel functions; Analytic sets |
8 |
| |
1.6 |
Densities; First category sets |
9 |
| |
1.7 |
The Baire Category Theorem; Romanovski's Lemma |
10 |
| |
1.8 |
Vitali's Covering Theorem |
11 |
| |
1.9 |
The generalized properties PG, [PG], P1;P2G |
11 |
| |
1.10 |
Extreme derivatives |
13 |
| |
1.11 |
Approximate continuity and derivability |
14 |
| |
1.12 |
Sharp derivatives D#F |
15 |
| |
1.13 |
Local systems; examples |
16 |
| |
1.14 |
 -open sets -open sets |
19 |
| |
1.15 |
Semicontinuity; -semicontinuity -semicontinuity |
21 |
| 2 |
|
Classes of functions |
25 |
| |
2.1 |
Darboux conditions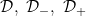 |
25 |
| |
2.2 |
Baire conditions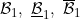 |
27 |
| |
2.3 |
Conditions![\small{\mathcal C}_i; ~{\mathcal C}_i^*; ~[{\mathcal C}_i G];~ [{\mathcal C}G] \small{\mathcal C}_i; ~{\mathcal C}_i^*; ~[{\mathcal C}_i G];~ [{\mathcal C}G]](http://latex.codecogs.com/gif.latex?%5Csmall%7B%5Cmathcal%20C%7D_i%3B%20~%7B%5Cmathcal%20C%7D_i%5E%2A%3B%20~%5B%7B%5Cmathcal%20C%7D_i%20G%5D%3B~%20%5B%7B%5Cmathcal%20C%7DG%5D) |
31 |
| |
2.4 |
Conditions internal, internal*,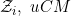 |
33 |
| |
2.5 |
Conditions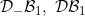 |
36 |
| |
2.6 |
Conditions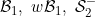 and and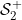 - local systems - local systems |
39 |
| |
2.7 |
Conditions VB, VB, VBG, |
41 |
| |
2.8 |
Conditions VB*, VB*, VB*G |
44 |
| |
2.9 |
Conditions monotone* and VB* |
47 |
| |
2.10 |
Conditions VB*, VB*G and![\small{\mathcal D}, ~{\mathcal D}_-, ~[{\mathcal C}G], ~ [{\mathcal C}G] \small{\mathcal D}, ~{\mathcal D}_-, ~[{\mathcal C}G], ~ [{\mathcal C}G]](http://latex.codecogs.com/gif.latex?%5Csmall%7B%5Cmathcal%20D%7D%2C%20~%7B%5Cmathcal%20D%7D_-%2C%20~%5B%7B%5Cmathcal%20C%7DG%5D%2C%20~%20%5B%7B%5Cmathcal%20C%7DG%5D) , lower internal, internal , lower internal, internal |
50 |
| |
2.11 |
Conditions AC, ACG |
51 |
| |
2.12 |
Conditions AC*, AC*, AC*G, AC*G |
54 |
| |
2.13 |
Conditions L, L, LG, LG |
58 |
| |
2.14 |
Summability and conditions VB and AC |
60 |
| |
2.15 |
Differentiability and conditions VBG, VB*G |
62 |
| |
2.16 |
A fundamental lemma for monotonicity |
65 |
| |
2.17 |
Krzyzewski's lemma and Foran's lemma |
70 |
| |
2.18 |
Conditions (N), T1, T2, (S), (+), (-) |
71 |
| |
2.19 |
Conditions wS, wN |
78 |
| |
2.20 |
Condition (N) |
78 |
| |
2.21 |
Conditions N∞ , N+∞, N-∞ |
79 |
| |
2.22 |
Conditions M*,M* |
82 |
| |
2.23 |
Conditions (M), M , Ng∞ , Ng+∞ |
84 |
| |
2.24 |
Derivation bases |
87 |
| |
2.25 |
Conditions ACD#, ACDo, ACD |
88 |
| |
2.26 |
Conditions YD#, YDo, YD |
89 |
| |
2.27 |
Characterizations of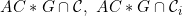 , AC and AC , AC and AC |
90 |
| |
2.28 |
Conditions ACn, ACω , AC∞ ,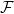 |
93 |
| |
2.29 |
Conditions VBn, VBω , VB∞ , 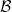 |
96 |
| |
2.30 |
Variations Vn, Vω , V∞ and the Banach Indicatrix |
100 |
| |
2.31 |
Conditions So, wSo and AC∞ , VB∞ , (N) |
103 |
| |
2.32 |
Conditions Ln, Lω , L∞ ,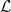 |
104 |
| |
2.33 |
Conditions ΛZ, f.l., σ.f.l. |
108 |
| |
2.34 |
Conditions SACn, SACω, SAC∞,,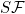 |
111 |
| |
2.35 |
Conditions SVBn, SVBω, SVB∞,,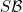 |
114 |
| |
2.36 |
Conditions DWn, DWω , DW∞ , DW* |
116 |
| |
2.37 |
Conditions En, Eω, E∞,,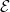 |
118 |
| |
2.38 |
Conditions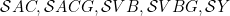 |
121 |
| 3 |
|
Finite representations for continuous functions |
127 |
| |
3.1 |
quasi-derivable ⊆ AC*; DW*G + AC*; DW*G and approximately quasi-derivable ⊆ AC; DW1G+AC; DW1G |
127 |
| |
3.2 |
 ⊆ DW1+DW1 on a perfect nowhere dense set ⊆ DW1+DW1 on a perfect nowhere dense set |
130 |
| |
3.3 |
Wrinkled functions (W) and condition (M) |
131 |
| |
3.4 |
 = quasi-derivable + quasi-derivable = quasi-derivable + quasi-derivable |
134 |
| |
3.5 |
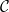 = AC*; DW1G+AC*; DW1G+AC*; DW1G = AC*; DW1G+AC*; DW1G+AC*; DW1G |
135 |
| 4 |
|
Monotonicity |
141 |
| |
4.1 |
Monotonicity and conditions (-), VBωG, 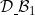 |
141 |
| |
4.2 |
Monotonicity and conditions (M), uCM, AC, 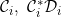 |
142 |
| |
4.3 |
Monotonicity and conditions N-∞; N∞ |
145 |
| |
4.4 |
Local monotonicity |
149 |
| |
4.5 |
 -derivatives and the Mean Value Theorem -derivatives and the Mean Value Theorem |
149 |
| |
4.6 |
Relative monotonicity |
151 |
| |
4.7 |
An application of Corollary 4.4.1 |
151 |
| |
4.8 |
A general monotonicity theorem |
152 |
| |
4.9 |
Monotonicity in terms of extreme derivatives |
158 |
| 5 |
|
Integrals |
161 |
| |
5.1 |
Descriptive and Perron type definitions for the Lebesgue integral |
161 |
| |
5.2 |
Ward type definitions for the Lebesgue integral |
166 |
| |
5.3 |
Henstock variational definitions for the Lebesgue integral |
167 |
| |
5.4 |
Riemann type definitions for the Lebesgue integral (The McShane integral) |
169 |
| |
5.5 |
Theorems of Marcinkiewicz type for the Lebesgue integral |
172 |
| |
5.6 |
Bounded Riemann# sums; locally small Riemann# sums |
173 |
| |
5.7 |
Descriptive and Perron type definitions for the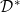 -integral -integral |
174 |
| |
5.8 |
An improvement of the Hake Theorem |
180 |
| |
5.9 |
An improvement of the Looman-Alexandroff Theorem. The equivalence of the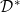 -integral and the (Pj,k)-integral -integral and the (Pj,k)-integral |
184 |
| |
5.10 |
Ward type definitions for the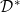 -integral -integral |
186 |
| |
5.11 |
Henstock variational definitions for the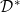 -integral -integral |
187 |
| |
5.12 |
The Kurzweil-Henstock integral |
188 |
| |
5.13 |
Cauchy and Harnak extensions of the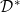 -integral -integral |
189 |
| |
5.14 |
A theorem of Marcinkiewicz type for the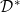 -integral -integral |
190 |
| |
5.15 |
Bounded Riemann sums and locally small Riemann sums |
192 |
| |
5.16 |
Riemann type integrals and local systems |
193 |
| |
5.17 |
The <LPG> and <LDG> integrals |
197 |
| |
5.18 |
The chain rule for the derivative of a composite function |
200 |
| |
5.19 |
The chain rule for the approximate derivative of a composite function |
202 |
| |
5.20 |
Change of variable formula for the Lebesgue integral |
204 |
| |
5.21 |
Change of variable formula for the Denjoy*-integral |
205 |
| |
5.22 |
Change of variable formula for the <LDG>integral |
206 |
| |
5.23 |
Integrals of Foran type |
207 |
| |
5.24 |
Integrals which extend both, Foran's integral and Iseki's integral |
210 |
| 6 |
|
Examples |
213 |
| |
6.1 |
The Cantor ternary set, a perfect nowhere dense set |
213 |
| |
6.2 |
The Cantor ternary function φ |
214 |
| |
6.3 |
A real bounded So+ closed set which is not of Fσ-type |
214 |
| |
6.4 |
An So+ lower semicontinuous function which is not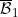 |
215 |
| |
6.5 |
A function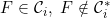 |
215 |
| |
6.6 |
A function![\small F \in {\mathcal D}, ~F \in [{\mathcal C}_i^*G], ~ F \notin [{\mathcal C}G] \small F \in {\mathcal D}, ~F \in [{\mathcal C}_i^*G], ~ F \notin [{\mathcal C}G]](http://latex.codecogs.com/gif.latex?%5Csmall%20F%20%5Cin%20%7B%5Cmathcal%20D%7D%2C%20~F%20%5Cin%20%5B%7B%5Cmathcal%20C%7D_i%5E%2AG%5D%2C%20~%20F%20%5Cnotin%20%5B%7B%5Cmathcal%20C%7DG%5D) |
215 |
| |
6.7 |
A function ![\small F \in {\mathcal D B}_1,~F\notin [{\mathcal C}G] \small F \in {\mathcal D B}_1,~F\notin [{\mathcal C}G]](http://latex.codecogs.com/gif.latex?%5Csmall%20F%20%5Cin%20%7B%5Cmathcal%20D%20B%7D_1%2C~F%5Cnotin%20%5B%7B%5Cmathcal%20C%7DG%5D) |
216 |
| |
6.8 |
A function F ∈ uCM; F ∉ lCM |
216 |
| |
6.9 |
A function concerning conditions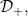 , CM, sCM, lower internal , CM, sCM, lower internal |
217 |
| |
6.10 |
A function concerning conditions 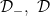 , internal, , internal,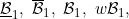 [VBG], (-), T1, T2 (Bruckner) [VBG], (-), T1, T2 (Bruckner) |
217 |
| |
6.11 |
A function concerning conditions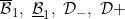 , lower internal, internal, internal* (Dirichlet) , lower internal, internal, internal* (Dirichlet) |
|
| |
6.12 |
A function concerning conditions: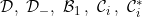 , lower internal, internal*, VB, VB*G, N-∞ , lower internal, internal*, VB, VB*G, N-∞ |
|
| |
6.13 |
A function 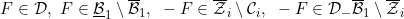 |
|
| |
6.14 |
A function 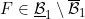 , F ∈ lower internal, , F ∈ lower internal,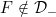 |
220 |
| |
6.15 |
A function F ∈ sCM, F ∉ internal* |
220 |
| |
6.16 |
A function F ∈ AC*G \ AC, 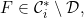 F ∈ sCM \ internal* F ∈ sCM \ internal* |
220 |
| |
6.17 |
A function F ∈ (D.C.),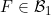 , F ∉ m2, , F ∉ m2, 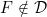 |
221 |
| |
6.18 |
A function F ∈ (+) ∩ (-); 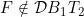 |
221 |
| |
6.19 |
A function 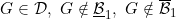 , G'ap(x) exists n.e., G'ap(x) ≥ 0 a.e. (Preiss) , G'ap(x) exists n.e., G'ap(x) ≥ 0 a.e. (Preiss) |
222 |
| |
6.20 |
A function 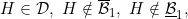 H'ap(x) exists on (0,1) (Preiss) H'ap(x) exists on (0,1) (Preiss) |
222 |
| |
6.21 |
A function 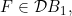 F(x) = 0 a.e., F is not identically zero (Croft) F(x) = 0 a.e., F is not identically zero (Croft) |
223 |
| |
6.22 |
A function ![\small F \in {\mathcal D}, ~F \in [{\mathcal C}G] \small F \in {\mathcal D}, ~F \in [{\mathcal C}G]](http://latex.codecogs.com/gif.latex?%5Csmall%20F%20%5Cin%20%7B%5Cmathcal%20D%7D%2C%20~F%20%5Cin%20%5B%7B%5Cmathcal%20C%7DG%5D) , F ∈ [VBG], F ∉ VB*G, , F ∈ [VBG], F ∉ VB*G, 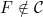 (Bruckner) (Bruckner) |
223 |
| |
6.23 |
A function F ∈ AC*, F ∉ VB* |
224 |
| |
6.24 |
A function F ∈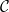 , F ∈ T1, F ∈ VBG, F ∉ VB*G , F ∈ T1, F ∈ VBG, F ∉ VB*G |
224 |
| |
6.25 |
A function F ∈ [bAC*G] ∩ VB*G N-∞, F ∉ lower internal |
225 |
| |
6.26 |
A function F ∈ C ∩ (S) ∩ LG, F ∉ AC*G, F'(x) does not exist on a set of positive measure, F(x)+x ∈ LG, F(x)+x ∉ T1 |
225 |
| |
6.27 |
A function F ∈ (S) ∩ C such that the sum of F and any linear nonconstant function does not satisfy (N) (Mazurkievicz) |
226 |
| |
6.28 |
A function F ∈ (M), F ∉ T2 |
227 |
| |
6.29 |
Functions concerning conditions (M), AC, T1, T2, (S), (N), L, L2G, VBG,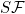 , quasi-derivable , quasi-derivable |
229 |
| |
6.30 |
A function G ∈ N∞ , F ∉ (M), F ∉ (+) |
237 |
| |
6.31 |
Functions concerning conditions (S), (N), (M), T1, T2, ACG, ACn, SACn, VB2, VBG, SVB, 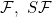 |
238 |
| |
6.32 |
A function F ∈ lower semicontinuous, F ∈ AC2, F ∉ AC |
244 |
| |
6.33 |
A function Fn ∈ Ln+1 on a perfect set, Fn ∈ VBn on no portion of this set, Fn ∈ Ln+1G, Fn ∉ ACnG on [0,1] |
245 |
| |
6.34 |
Functions F ∈ L_2G, Gs ∈ (N), G's = F' a.e., Gs-F is not identically zero, F ∉ SACG |
247 |
| |
6.35 |
A function F ∈ L2, F ∉ T2, F ∉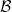 |
250 |
| |
6.36 |
A function F ∈ VB2 on C, V2(F;C) \≤ 1 |
252 |
| |
6.37 |
A function Fp ∈ L2p, Fp ∉ AC2p-1, Fp ∈ VB2 on C, V2(Fp;C) ≤ 1 |
252 |
| |
6.38 |
A function G ∈ VB2, G ∉ ACn on C, G ∈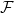 on [0,1] on [0,1] |
254 |
| |
6.39 |
A function F1 ∈ VB2 on C, V2(F1;[0,x] ∩ C) = φ(x) (G. Ene) |
254 |
| |
6.40 |
A function Fq ∈ (N) on [0,1], Fq ∉ VBn on C, Fq ∈ VBω on C (G. Ene) |
255 |
| |
6.41 |
A function G1 ∈ L2G, G1 ∈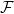 , G1 ∉ SVBG, G1 ∉ SACG, (G1)'ap does not exist on a set of positive measure , G1 ∉ SVBG, G1 ∉ SACG, (G1)'ap does not exist on a set of positive measure |
256 |
| |
6.42 |
A function F ∈ SACG, F ∉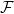 , F ∉ ACG , F ∉ ACG |
258 |
| |
6.43 |
A function F ∈ DW1, F ∉ DW* |
261 |
| |
6.44 |
A function F ∈ AC*;DW1G, F ∉ AC*;DW*G |
261 |
| |
6.45 |
Functions F1,F2 ∈ C ∩ AC*;DW*G, F1, F2 are derivable a.e., F'1 = F'2 a.e., F1 and F2 do not differ by a constant |
262 |
| |
6.46 |
Functions F1,F2 ∈ C ∩ AC*;SW_1G, F1,F2 are approximately derivable a.e., F1+F2 ∉ quasi-derivable |
262 |
| |
6.47 |
Functions F1,F2 ∈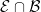 , F1,F2 ∉ , F1,F2 ∉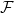 , F1+F2 ∉ , F1+F2 ∉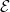 |
264 |
| |
6.48 |
A function Gn ∈ En+1, Gn ∉ En, Gn ∈ Ln2 + 2n+1, Gn ∉ VBn2+2n |
265 |
| |
6.49 |
Functions concerning conditions L,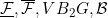 , E1G , E1G |
268 |
| |
6.50 |
A function F ∈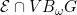 , F ∉ , F ∉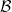 |
270 |
| |
6.51 |
A function F ∈ (N), F ∉ ΛZ (Foran) |
271 |
| |
6.52 |
A function F ∈ AC º ΛZ, F ∉ ΛZ (Foran) |
272 |
| |
6.53 |
A function H ∈ AC+ΛZ, H ∉ ΛZ (Foran) |
272 |
| |
6.54 |
A function G ∈ AC · ΛZ, G ∉ ΛZ (Foran) |
272 |
| |
6.55 |
A function F1 ∈ AC, F1 ∉ Ln, F1 ∉ 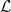 |
273 |
| |
6.56 |
Functions F1 ∈ AC2G, F2 ∈ ΛZ, F1+F2 ∉ (M), F1' = -F2' a.e. |
273 |
| |
6.57 |
A function F ∈ ΛZ, F ∉![\small [{\mathcal E}] \small [{\mathcal E}]](http://latex.codecogs.com/gif.latex?%5Csmall%20%5B%7B%5Cmathcal%20E%7D%5D%20) |
274 |
| |
6.58 |
Functions F1 ∈ (S), F1 ∈ AC º σ.f.l. F1 ∉ σ.f.l., F2 ∈ L, F1+F2 ∉ T2 |
276 |
| |
6.59 |
Functions G1 ∈ σ.f.l., G2 ∈ AC, G1+G2 ∉ σ.f.l. |
279 |
| |
6.60 |
Functions H1 ∈ σ.f.l., H2 ∈ AC, H1 · H2 ∉ σ.f.l. |
280 |
| |
6.61 |
A function F ∈ σ.f.l., F ∈ T1, F ∉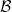 , F is nowhere approximately derivable (Foran) , F is nowhere approximately derivable (Foran) |
280 |
| |
6.62 |
A function G ∈ σ.f.l. ∩ T1, G is nowhere derivable, G'ap(x) = 0 a.e., G ∉ W, G ∈ W* (Foran) |
284 |
| |
6.63 |
A function F ∈ W on a perfect nowhere dense set of positive measure with each level set perfect, F is nowhere approximately derivable |
287 |
| |
6.64 |
A function G1 ∈ DW1 ∩ C, G1 is not approximately derivable a.e. on a set of positive measure |
291 |
| |
6.65 |
A function F ∈ C, F is quasi-derivable, F ∉ AC º AC + AC |
291 |
| |
6.66 |
Examples concerning the chain rule for the approximate derivative of a composite function |
291 |
| |
|
Bibliography |
293 |
| |
|
Index |
305 |
|
|
 |
|